Understanding Quadratic Equations

Quadratic equations are integral to mathematics, offering insights into various disciplines such as physics, engineering, and economics. A quadratic equation is a second-degree polynomial equation in a single variable x, with a standard form of (ax^2 + bx + c = 0), where (a), (b), and (c) are constants, and (a \neq 0). The solutions to this equation, known as roots, are the x-values where the parabola (the graph of a quadratic equation) intersects the x-axis.

Methods of Solving Quadratic Equations

1. Factoring

Factoring involves expressing the quadratic equation in a product of two binomials. This method is efficient when the equation can easily be factored into simpler, factorable expressions. The general approach is to rewrite the middle term to find two numbers that multiply to give (ac) (product of (a) and (c)) and add to give (b). Once factored, each binomial is set equal to zero to solve for (x).

Example:

Consider (x^2 – 5x + 6 = 0). This can be factored as ((x-2)(x-3) = 0). Setting each factor to zero gives the roots as (x = 2) and (x = 3).

2. Completing the Square

Completing the square transforms a quadratic equation into a perfect square trinomial, making it easier to solve. The process involves adding and subtracting a certain number to both sides of the equation to form a square on one side.

Steps:

• Ensure the coefficient of (x^2) is 1. If not, divide the entire equation by (a).
• Move the constant term to the other side of the equation.
• Add ((\frac{b}{2})^2) to both sides of the equation, where (b) is the coefficient of (x).
• Write the left side as a square of a binomial.
• Solve for (x) by taking the square root of both sides and then isolating (x).

Example:

For (x^2 – 6x + 5 = 0), first subtract 5 from both sides to get (x^2 – 6x = -5). Add ((\frac{-6}{2})^2 = 9) to both sides to complete the square: (x^2 – 6x + 9 = 4). This simplifies to ((x-3)^2 = 4), and taking square roots gives (x – 3 = \pm 2), hence (x = 3 \pm 2), leading to (x = 1) or (x = 5).

3. Quadratic Formula

The quadratic formula provides a direct way to find the roots of any quadratic equation. It is derived from the process of completing the square and is applicable to all quadratic equations.

The Formula:

The roots of the equation (ax^2 + bx + c = 0) are given by:

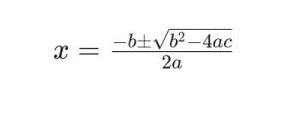
Example:

Given (2x^2 – 4x – 6 = 0), applying the quadratic formula yields:

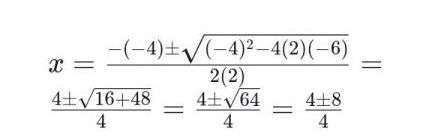
Practice Problems

1. Solve (x^2 – 7x + 12 = 0) using factoring.
2. Use completing the square to solve (x^2 – 10x + 21 = 0).
3. Apply the quadratic formula to find the roots of (3x^2 – 2x – 5 = 0).

Solutions to Practice Problems

1. Factoring: (x^2 – 7x + 12 = 0) factors to ((x-3)(x-4) = 0), giving (x = 3, 4).
2. Completing the Square: For (x^2 – 10x + 21 = 0), moving 21 to the other side and completing the square yields (x = 5 \pm \sqrt{4}), so (x = 5, 1).

3. Quadratic Formula: Applying the quadratic formula to (3x^2 – 2x – 5 = 0), we get:

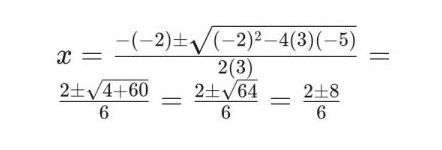
Deepening Understanding

Solving quadratic equations is a foundational skill in algebra that opens the door to understanding more complex mathematical concepts. The methods of factoring, completing the square, and using the quadratic formula each have their unique applications and are chosen based on the specific characteristics of the equation at hand.

Applications of Quadratic Equations

Quadratic equations are not just academic exercises but have real-world applications in various fields such as physics, engineering, and economics. For instance, they are used to model projectile motion, calculate optimal profit or cost in business scenarios, and solve for rates of reaction in chemistry.

Challenges and Tips

• Choosing the Right Method: Factoring is quickest when it is straightforward to identify the factors. If the equation does not easily factor, the quadratic formula is a reliable universal method. Completing the square is particularly useful when dealing with equations in calculus and when deriving the quadratic formula itself.
• Practicing Word Problems: Applying these concepts to solve word problems can enhance understanding and application skills. Try converting real-life situations into quadratic equations and solving them.
• Review and Practice: Regularly review the underlying concepts and practice solving equations using all three methods. Variety in practice problems helps in reinforcing the concepts.

Conclusion

Quadratic equations are a crucial part of high school mathematics. Mastering the various methods of solving these equations not only aids in academic success but also builds a foundation for future mathematical learning. Whether through factoring, completing the square, or applying the quadratic formula, understanding how to manipulate these equations opens up a world of possibilities for solving complex problems. Remember, mathematics is not just about finding the right answer but understanding the process that leads you there. Keep practicing, and soon, solving quadratic equations will become second nature.